Themen

1 Einleitung

Preuss & Reimann mahnen ausdrücklich vor einer unbedachten Einführung des Orbitalmodells. Alleine der Begriff des „Orbitals“ werde in Schulen häufig so nachlässig gehandhabt, dass sie sogar dafür plädieren, auf das Orbitalmodell im Oberstufenunterricht gänzlich zu verzichten (Preuss, & Reimann, 1990). Christen nimmt diesen Gedanken auf, gleichwohl sieht er aber doch noch Möglichkeiten das Orbitalmodell sowie das Hybridisierungskonzept mit Jugendlichen in einem Leistungskurs der Sekundarstufe II bei angemessener didaktischer Reduktion erfolgreich zu bearbeiten. Dazu schreibt er in einem Aufsatz der CHEMKON: "Diese "Hybridisierung" ist also kein Vorgang, sondern eine mathematische Operation mit dem Zweck, aus den Atomorbitalen (Ψ-Funktionen) Funktionen zu erhalten, die nachher für die Bildung lokalisierter MO besser verwendet werden können als die Ein-Elektronen-AO  2s, 2p_x, 2p_y, 2p_z. Anders gesagt, mit der "Hybridisierung" bildet man aus den Atomorbitalen durch eine mathematische Transformation Hybrid-Orbitale, die nach der linearen Kombination mit AO [oder Hybridorbitalen] anderer Atome (hier z.B. der vier 1s-AO der Wasserstoffatome) zur Beschreibung der tatsächlichen Konstitution eines Moleküls geeignet sind, die aber keinesfalls die Molekülgeometrie oder die Bindungswinkel erklären ..." (Christen, 1996).

Zweifelsohne befinden wir uns mit dem Orbitalmodell auf Teilchenebene, jedoch darf die Grenze zur Teilcheneigenschaft keinesfalls überschritten werden. So verbietet sich beispielsweise die Aussage, die Carbonylgruppe sei planar, weil das Carbonylkohlenstoffatom sp²-hybridisiert sei! Die räumliche Anordnung der Atome in einem Molekül ist messbar, das Modell hingegen erlaubt wieder nur eine sehr gute Beschreibung der Bindungsverhältnisse (Christen & Meyer, 1997; Gewehr, 2020). Dementsprechend schlagen wir für den Unterricht eine andere Formulierung vor, die den experimentellen Befund an die erste Stelle rückt, gefolgt von dem durch das Hybridisierungskonzept erweiterten Orbitalmodell. Beispiel: Mit Hilfe der Röntgenstrukturanalyse hat man gefunden, dass im Aceton-Molekül die Kohlenstoffatome beider Methylreste sowie die Atome der Carbonylgruppe in einer Ebene liegen. Zur modellhaften Beschreibung der Bindungsverhältnisse im Molekül nimmt man für das Kohlenstoffatom der Carbonylgruppe sp²-Hybridorbitale an, deren räumliche Orientierung den gemessenen Bindungswinkeln entspricht.

2 Zur Entwicklung der Atomvorstellung

2.1 Verschiedene Atommodelle im Chemieunterricht

Orbital- und Hybridisierungsmodell sind so leistungsstark, dass mit deren Hilfe gezielte Synthesen von Stoffen mit definierter Struktur der sie aufbauenden Moleküle möglich geworden sind. Nicht zuletzt deswegen fordern (fast) alle Lehrpläne der verschiedenen Bundesländer für den Chemieunterricht in der Sekundarstufe II eine vertiefte Behandlung von Atombau und chemischer Bindung, einhergehend mit der Entwicklung der Atommodelle. Von entscheidender Bedeutung ist dabei, dass die Schüler/innen den Weg der Erkenntnisgewinnung ausgehend von experimentellen Befunden hin zur Weiterentwicklung der Modellvorstellungen verstehen. Mit Hilfe des Rutherford‘schen Streuversuchs gelingt dies bei der Einführung des Kern-Hülle-Modells sehr gut. Auch die gegenseitige Abstoßung von Bindungselektronenpaaren (und freien Elektronenpaaren) stellt eine nachvollziehbare Grundlage für das EPA-Modell dar. Absorptions- und Emissionsspektren veranlassten N. Bohr seine Elektronenbahnen zu postulieren, ein schönes Beispiel dafür, dass sich eine noch so anschauliche Atomvorstellung durch später erzielte experimentelle Ergebnisse als falsch herausstellte. Im weiterführenden Chemieunterricht gilt es, diese vermeintlich präzisen Modelle abzulösen durch Wahrscheinlichkeitsaussagen zum Aufenthalt von Elektronen (Heisenberg, Born). Vermieden werden sollte dabei auf jeden Fall eine "pseudoanschauliche" Aussage, nach der man sich etwa "Elektronen als winzig kleine Kugeln vorstellen könne, die in den Orbitalen (Räumen?) herum kullern". Diese fachlich falsche Formulierung scheitert spätestens bei der Betrachtung von z.B. p-Orbitalen, deren Teile durch eine Knotenfläche voneinander getrennt sind (Aufenthaltswahrscheinlichkeit gleich Null).

2.2 Atommodelle in Lehrbüchern

Die Beschreibungen und Darstellungen zu den bislang genannten Modellen gelingen in den gängigen Schulbüchern recht gut. Für die Kapitel zum Orbitalmodell und hier speziell zur Einführung des Hybridisierungsmodells trifft dies leider nicht mehr zu.
Bei vielen Autoren kann man lesen, dass bei der Hybridisierung Orbitale miteinander vermischt werden oder gar verschmelzen. Dieses „Vermischen“ bleibt für die meisten Schüler/innen unverständlich, womöglich auch dadurch begründet, dass unzulässige Vorstellungen vom Wesen bzw. der Beschaffenheit eines Orbitals, wie oben bereits beispielhaft beschrieben, zu falschen Schlussfolgerungen führen. So tauchen in Schülerköpfen u.U. Fragen auf, wie man denn Räume oder gar Aufenthaltswahrscheinlichkeiten miteinander mischen könnte. Auch der Begriff „verschmelzen“ muss zu Fehlinterpretationen führen, da mit dieser Vokabel gänzlich andere Verknüpfungen assoziiert werden. Diese Verständnisschwierigkeiten gilt es zu vermeiden, damit die Lernenden den Modellcharakter der Orbitale nicht nur verstehen, sondern im Nachgang auch korrekt anwenden können.

Interessierten Kolleg/inn/en empfehlen wir zur Einarbeitung in das Thema sowie zur Vorbereitung ihres Unterrichts wärmstens die Grundlagen der Allgemeinen und Anorganischen Chemie von Christen & Meyer (1997), hier besonders das Kapitel zur chemischen Bindung. Noch wesentlich ausführlicher als in dem eingangs zitierten Aufsatz von Christen legen die Autoren dar, dass sowohl das Orbital- als auch das Hybridisierungsmodell nur zur Beschreibung der vorab experimentell bestimmten Molekülstrukturen verwendet werden soll.

2.3 Konstruktion eines sp-Hybridorbitals

Als wirkungsvolles Hilfsmittel konnten wir hier in vielen Chemie-Leistungskursen die Konstruktion eines sp-Hybridorbitals (Abb. 2) durch grafische Addition aus je einem s- und p-Orbital einsetzen (Abb. 1) (vgl. Dumbacher, 1977 und Christen & Meyer, 1997). Benutzt werden dabei Konturliniendiagramme, die mathematisch betrachtet Funktionswerten entsprechen (winkelabhängige Anteile).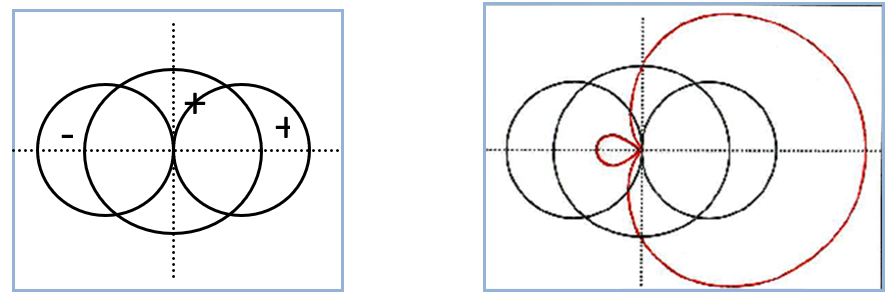

      

Abb. 1. Konturliniendiagramm eines s- und eines  p-Orbitals                 Abb. 2. Grafische Addition zu einem sp-Hybridorbital

Die in den Abbildungen verwendete Größe der Orbitaldarstellungen (s und p) sind frei gewählt, auch die vereinfachte Kreisform für die Teile des p-Orbitals ist zum Verständnis des Prinzips der Hybridisierung ausreichend. Mit enger Anleitung gelang es allen Schülern/innen ihre eigenen Hybridorbitale Punkt für Punkt selbst zu zeichnen. Der hierzu notwendige Zeitaufwand zugunsten einer intensiven Auseinandersetzung mit der Konstruktion ist nach unserer Einschätzung gerechtfertigt. Schließlich sollen die Schüler/innen aktiv zeichnend zur Einsicht gelangen, dass es sich bei der Hybridisierung nur um einen mathematischen Prozess und keineswegs um einen physikalischen Vorgang auf Teilchenebene handelt (Christen & Meyer, 1997). Weitgehend problemlos verlief dabei das Kombinieren der positiven Funktionswerte des s-Orbitals und des entsprechenden p-Orbitallappens im ersten Quadranten.

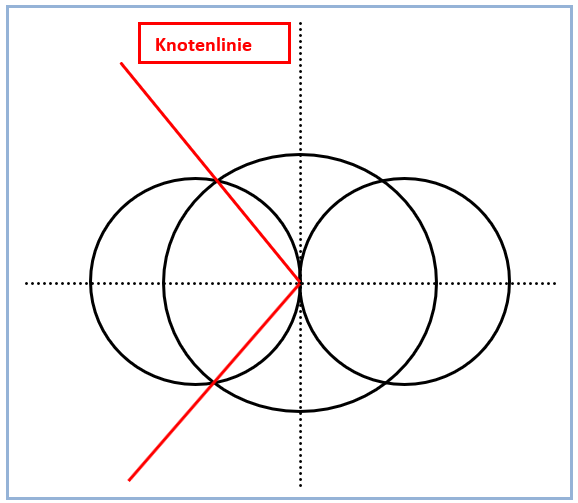
Abb. 3. Knotenlinien des zu konstruierenden sp-Hybridorbitals

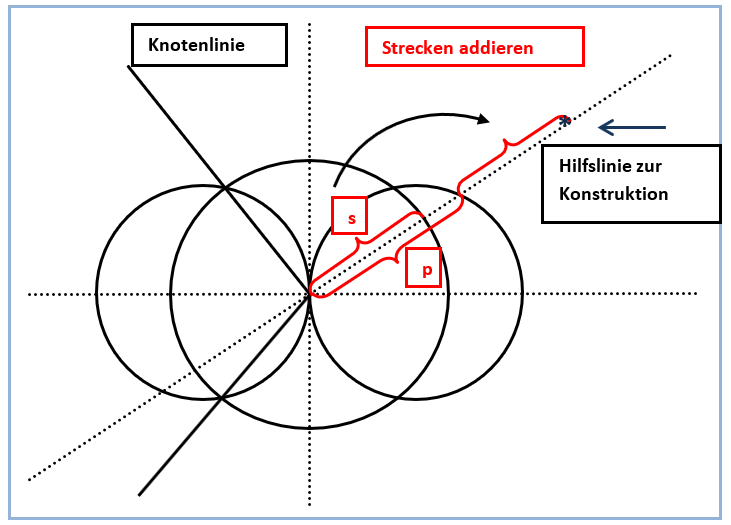
Abb. 4. Grafische Addition der Strecken  s  und  p  entlang einer Konstruktionshilfslinie

Letztlich müssen dabei nur Strecken auf den Hilfslinien ausgemessen und aufaddiert werden, wie in den Abbildungen 4 und 6 gezeigt. Auf diese Weise ergibt sich schnell die sinnfällige größere Ausdehnung des sp-Hybridorbitals in Richtung der zur Kombination verwendeten p-Orbital-Hälfte mit positiven Funktionswerten.

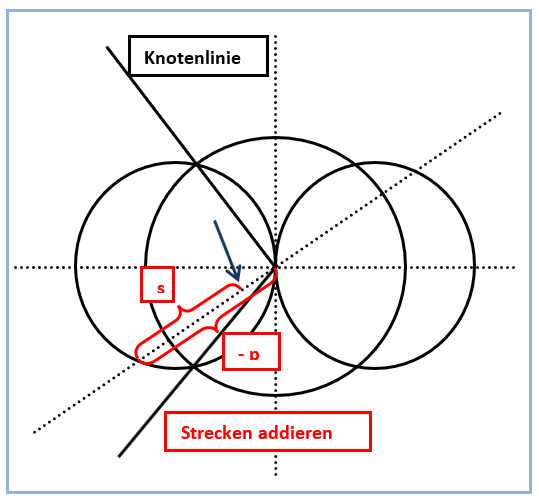
Abb. 5. Grafische Addition der Strecken  -p  und  s

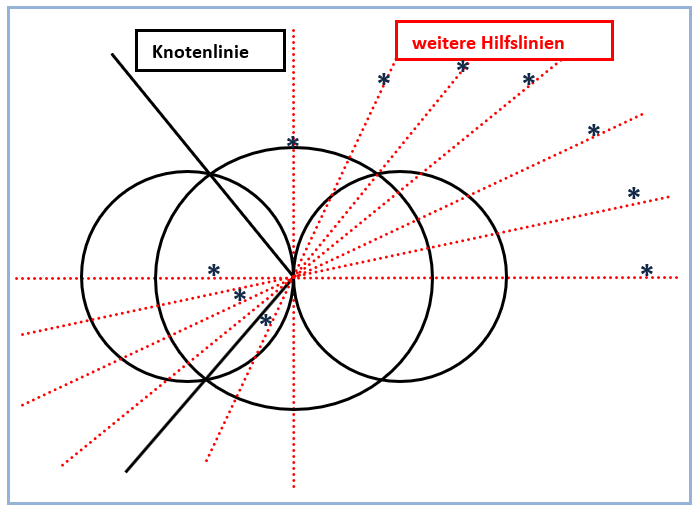
Abb. 6. Nutzung weiterer Hilfslinien zur Konstruktion

Etwas zeitaufwändiger gerät die Zeichnung des gegenüberliegenden kleinen Lappens des sp-Hybridorbitals. Hierbei gilt es zu beachten, dass die weiterhin positiven Funktionswerte des s-Orbitals mit den jetzt negativen Funktionswerten des anderen p-Orbitallappens verknüpft werden müssen (Abb. 5). Die Vorzeichen der Funktionswerte (+ und -) sind in Abbildung 1 vermerkt. Plus- und Minuszeichen haben also keineswegs etwas mit Ladungen zu tun. In der Praxis hat es sich bewährt, zunächst die Knotenlinien des sp-Hybridorbitals einzuzeichnen ^*). Diese beginnen im Ursprung des Koordinatensystems und verlaufen anschließend durch die Schnittpunkte der Konturlinien des s- und p-Orbitals (Abb. 3). Während die Konstruktion von Teilen des sp-Hybridorbitals im ersten und dritten Quadranten wie oben beschrieben nur durch Ausmessen und Addieren von Strecken gelingt, kann man die übrigen Teile durch Spiegeln an der x-Achse ergänzen und abschließen (Abb. 2).

^*) Räumlich betrachtet verlaufen diese Linien auf den Seiten eines Kegels, dessen Spitze im Ursprung des Koordinatensystems liegt. Die Kegelform ist die Folge davon, dass aus Gründen der Vereinfachung die beiden Teile des p-Orbitals als kreisförmig angenommen wurden. Bei Verwendung exakt berechneter Funktionswerte für das p-Orbital verläuft die Knotenfläche für das sp-Hybridorbital nicht durch den Atomkern (Hollemann & Wiberg, 1985).

Auch die Konstruktion eines sp²-Hybridorbitals aus einem s-Orbital und zwei aufeinander senkrecht stehenden p-Orbitalen ist mit Hilfe des gleichen Verfahrens möglich. Von der Zeichnung eines sp²-Hybridorbitals während des Unterrichts haben wir in Anbetracht des erheblichen Zeitaufwandes in der Regel abgesehen. So stellt diese Erweiterung für die Lernenden nichts wesentlich Neues dar, effizienter erwies sich hier die Vorlage einer vorgefertigten Konstruktion bzw. von Abbildungen aus der Literatur. Gut erkennbar ist die räumliche Orientierung des sp²-Hybridorbitals in Richtung der Winkelhalbierenden, außerdem sieht man die deutlich größere Ausdehnung im Vergleich mit einem sp-Hybridorbital. Darauf kann man später gewinnbringend zurückgreifen, wenn es darum geht die verschiedenen experimentell gemessenen C-C-Bindungsabstände im Ethan-, Ethen- bzw. Ethin-Molekül zu beschreiben.

2.4 Hybridisierung mit Hilfe von GeoGebra

Eine elegante Möglichkeit zur Konstruktion eines sp-Hybridorbitals ergibt sich bei der Anwendung von GeoGebra (https://www.geogebra.org/m/rt8khdc3 ; die Anwendung wurde von Christian Schlick erstellt). Das zeitintensive aber überaus lohnende Skizzieren von Hand lässt sich bei entsprechender Vorbereitung des Zeichenprogramms in Sekundenschnelle mit einem Finger an einem interaktiven Whiteboard demonstrieren. Durch kreisförmiges Ziehen des auf der Geraden liegenden Punktes  E  entwickelt sich gleichzeitig die Konturlinie des gewünschten sp-Hybridorbitals durch grafische Addition. Durch die Wahl verschiedener Farben kann man sehr gut die Bereiche unterscheiden, in denen Strecken addiert bzw. voneinander subtrahiert werden.

Wenngleich die Schüler/innen auf Nachfrage die Anwendung von GeoGebra als gleichermaßen praktisch und faszinierend bezeichneten, bevorzugten sie dennoch die, wenn auch zeitaufwändige, eigene Konstruktion mit Papier und Bleistift. Dadurch würden sie sich wesentlich intensiver mit dem Thema auseinandersetzen und den Sachverhalt auch besser verstehen. Aus diesen Gründen empfehlen wir die auch in diesem Aufsatz eingehaltene Reihenfolge bei der Bearbeitung des Themas im Unterricht, zuerst die eigene Erfahrung beim Zeichnen, danach die Demonstration mit GeoGebra. Eventuell als Additum bietet sich an, die Jugendlichen eine Vorhersage für das Aussehen eines sp²-Hybridorbitals treffen zu lassen bei nachfolgender Kontrolle mit Hilfe einer geeigneten Folie.

3 Ausblick

Wünschenswert wäre es, dass die in vielen Lehrbüchern enthaltenen Texte zum Hybridisierungsmodell mit teilweise diffusen und irreführenden Formulierungen unter Berücksichtigung der Grundsätze zur didaktischen Reduktion abgeändert würden. So sollte man hier auf die nicht messbare Energieaufnahme eines Elektrons beim nicht stattfindenden Hybridisierungsvorgang zum Erreichen eines nicht existierenden angeregten Zustandes gänzlich verzichten (Christen, 1996).  

Dazu gehören unseres Erachtens nicht nur eine eindeutige und unmissverständliche Fachsprache (Sieve & Hilker, 2019), auch eventuell notwendige Vereinfachungen dürfen den Sachverhalt, hier die Weiterentwicklung einer Modellvorstellung, nicht verfälschen. Letztlich muss diese anschlussfähig bleiben (Bauer & Bader, 2002).

Literatur

Bauer, H. F. & Bader, H. J. (2002). Prinzipien der Elementarisierung. In Pfeifer, P., Lutz, B. & Bader, H. J. (hg.), Konkrete Fachdidaktik Chemie (S. 187 - 190). München, Düsseldorf, Stuttgart: Oldenbourg.

Christen, H.R. (1996). Aus dem sp³-hybridisierten Zustand heraus geht das Kohlenstoffatom vier Bindungen ein … . Chemie Konkret, 3, 117 - 119.

Christen, H.R. & Meyer, G. (1997). Grundlagen der Allgemeinen und Anorganischen Chemie. Frankfurt, Aarau: Salle und Sauerländer.

Dumbacher, B. (1977). Übungen zur Vorlesung Physikalische Chemie I für LA Chemie. Universität Kaiserslautern. Vgl. auch Christen, H.R. & Meyer, G. (1997). Grundlagen der allgemeinen und anorganischen Chemie; Seite 84, Abb. 3.16. Frankfurt, Aarau: Salle und Sauerländer.

Geogebra. www.geogebra.org

Gewehr, M. (2020). Umgang mit Modellen im Chemieunterricht auf dem Didaktischen Prüfstand. MNU Journal 73(3), 260-262.

Hollemann, A.F. & Wiberg, E. (1985). Lehrbuch der Anorganischen Chemie. Berlin, New York: de Gruyter.

Preuß, H. & Reimann, A. (1990). Atom-und Molekülorbitale: eine Einführung. Frankfurt: Diesterweg.

Sieve,B. & Hilker, F. (2019). Wie sag ich’s meinem Kinde? Die Tücken (mit) der chemischen Fachsprache. Naturwissenschaften im Unterricht Chemie, 173, 6-7.

Autoren

Michael Gewehr, StD i.R., , Vogelsprung 6, 76835 Flemlingen. Ehem. Fachleiter für Chemie am Studienseminar in Speyer.

Christian Schlick, StD, , Im Sand 45, 67376 Harthausen.
Stellvertr. Schulleiter am Hans-Purrmann-Gymnasium in Speyer.